数据结构之数和二叉树

数据结构之树和二叉树

树和二叉树

树形结构
非线性结构：结点之间有分支、具有层次关系

树的定义

是n个结点的有限集
若n=0，称为空数，若n>0，则它满足以下两个条件：

(1)有且仅有一个特定的称为根的结点；

(2)其余节点可分为m(m>=0)个互不相交的有限集，其中每一个集合本身又是一棵树，称为根的子树 （递归的定义）

数的基本术语

有序数：树中结点的各子树从左至右有次序(最左边的为第一个孩子)
无序数：树中结点的各子树无次序

森林：是m（m>=0）棵互不相交的树的集合，把根结点删除数就变成了森林，一棵树可以看成是一个特殊的森林。

树结构和线性结构的比较

二叉树的定义

二叉树是n个结点的有限集，它或者是空集、或者由一个根结点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成

特点
每个结点最多有俩孩子（不存在度大于2的结点）
有左右之分，次序不能颠倒
二叉树可以是空集合，根可以有空的左子树或空的右子树

具有三个结点的二叉树有几种不同形态、普通树？

二叉树的五种基本形态

案例引入

案例一 数据压缩问题

案例二 利用二叉树求解表达式的值

树和二叉树的抽象数据类型定义

ADT BinaryTree{
   数据对象D：具有相同特性的数据元素的集合
   数据关系R：若D为空集，则R为空集
             若D非空，则R={H}；H是如下的二元关系  
             1.root唯一
             2.Dj并Dk为空集
             3...  
   基本操作P：
}ADT BinaryTree

基本操作P：

二叉树的性质和存储结构

性质1：在二叉树的第i层上至多有2的i-1次方个结点，至少有1个结点

性质2；深度为k的二叉树至多有2的k次方-1个结点，至少有k个结点

性质3：对任何一棵二叉树T，如果其叶子数为n0，度为2的结点数为n2，则n0=n2+1

满二叉树：一棵深度为k且有2的k次方-1个结点的二叉树称为满二叉树
特点：

完全二叉树
深度为k的具有n个结点的二叉树，当且仅当每一个结点都与深度为k的满二叉树中 的编号为1~n的结点一一对应时，称之为完全二叉数

完全二叉树的性质

性质4：具有n个结点的完全二叉树的深度为

性质5：

二叉树的顺序存储结构

实现：按满二叉树的节点层次编号，依次存放二叉树中的数据元素

//二叉树顺序存储表示
#define MAXSIZE 100
typedef TElemType SqBiTree[MAXSIZE];
SqBiTree bt;//定义名为bt的数组

二叉树的顺序储存缺点：

浪费空间，适用于满二叉树和完全二叉树

二叉树的链式存储结构

二叉链表表示法

typedef struct BiNode{
  TElemType data;
  struct BiNode *lchild,*rchild;//左右孩子指针
}BiNode,*BiTree;

在n个结点的二叉链中，有n+1个空指针域

三叉链表表示法

如果我们经常需要找前趋

typedef struct TriTNode{
  TElemType data;
  struct TriTNode *lchild,*rchild,*parent;//左右孩子指针
}TriTNode,*TriTree;

遍历二叉树

顺着某一条搜索路径寻访二叉树中的结点，使得每个结点均被访问过依次，且仅被访问一次
遍历目的：得到树中所有结点的一个线性排列，是树结构插入、删除、修改、查找和排序的前提

遍历方法

DLR：先序遍历
LDR：中序遍历
LRD：后序遍历

先序遍历二叉树

中序遍历二叉树

后序遍历二叉树

由二叉树的先序序列和中序序列、或由二叉树的后序序列和中序序列可以确定唯一一棵二叉树

例：已知先序和中序序列求二叉树

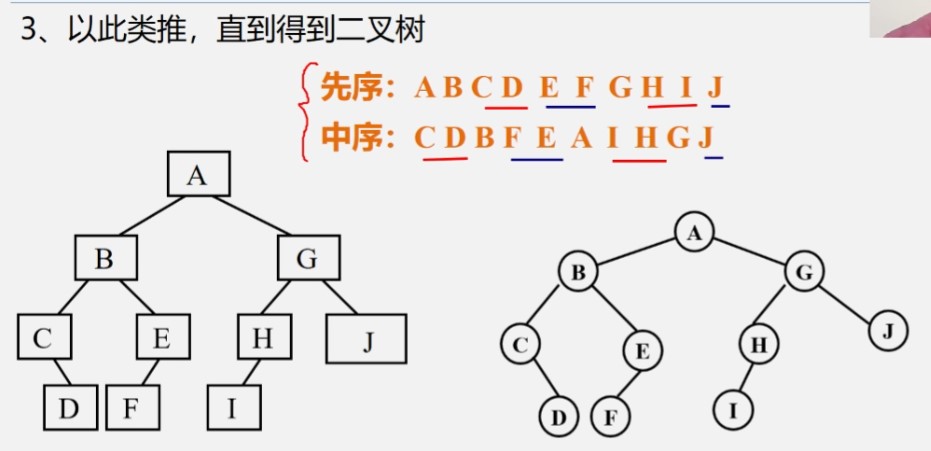
先序遍历二叉树-递归算法

Status PreOrderTraverse(BiTree T){
  if(T==NULL)return OK;
  else{
    visit(T);//访问根结点
    PreOrderTraverse(T->lchild);//递归遍历左子树
    PreOrderTraverse(T->rchild);//递归遍历右子树
  }
}

中序遍历二叉树-递归算法

Status InOrderTraverse(BiTree T){
  if(T==NULL)return OK;
  else{
    InOrderTraverse(T->lchild);//递归遍历左子树
    visit(T);//访问根结点
    InOrderTraverse(T->rchild);//递归遍历右子树
  }
}

后序遍历二叉树-递归算法

Status PostOrderTraverse(BiTree T){
  if(T==NULL)return OK;
  else{
    PostOrderTraverse(T->lchild);//递归遍历左子树
    PostOrderTraverse(T->rchild);//递归遍历右子树
    visit(T);//访问根结点
  }
}

遍历算法时间复杂度O(n)
遍历算法空间复杂度O(n)

中序遍历二叉树-非递归算法

二叉树中序遍历的非递归算法的关键：在中序遍历过某结点的整个左子树后，如何找到该节点的根与右子树

基本思想：
(1)建立一个栈
(2)根结点进栈，遍历左子树
(3)根结点出栈，输出根结点，遍历右子树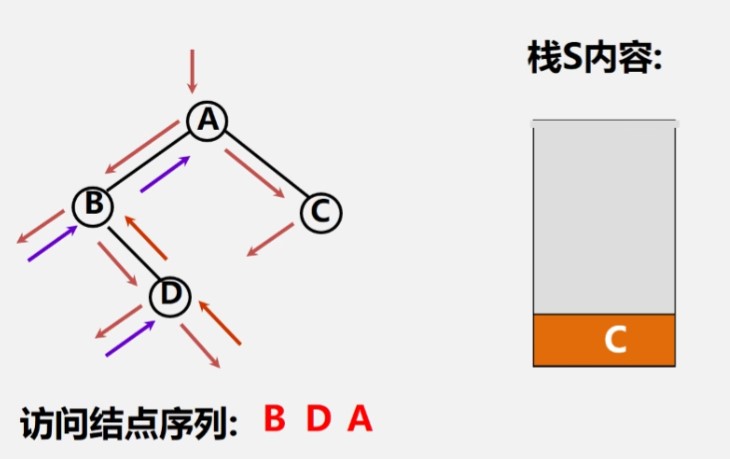

Status InOrderTraverse(BiTree T){
  BiTree p; InitStack(S);
  p=T;
  while(p||!StackEmpty(S)){
    if(p){
      Push(S,p);
      p=p->lchild;
    }
    else{
      Pop(S,q);
      printf("%c",q->data);
      p=q->rchild;
    }
  }
  return OK;
}

二叉树的层次遍历算法

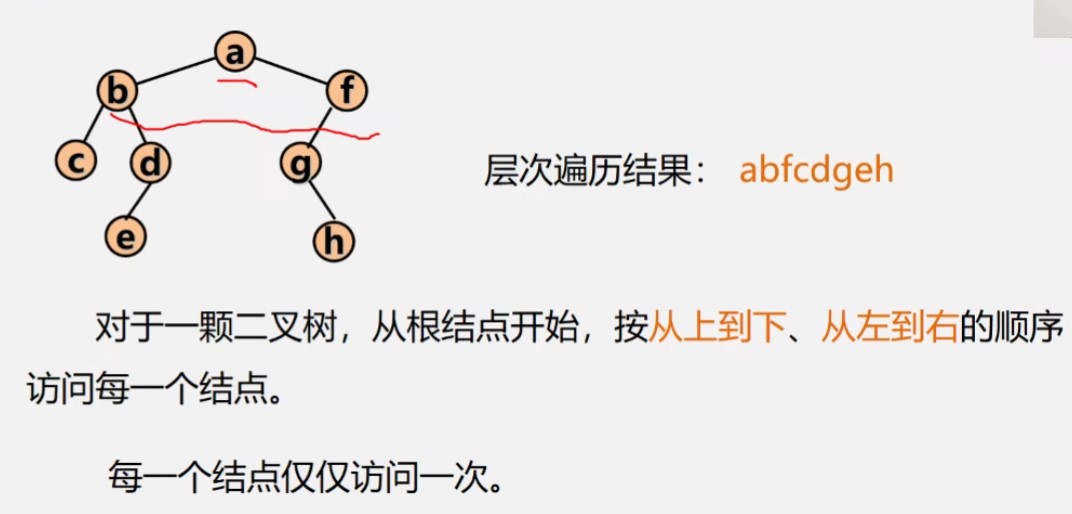
算法思路：
1.将根结点进队；
2.队不空时循环：从队列中出列一个结点*p,访问它；若它有左孩子结点，将左孩子结点进队，若它有右孩子结点，将右孩子结点进队

//使用队列类型的定义如下
typedef struct{
  BTNode data[MaxSize];//存放队中元素
  int front,rear;//队头和队尾指针
}SqQueue;

//二叉树层次遍历算法
void LevelOrder(BTNode *b){
  BTNode *p; SqQueue *qu;
  InitQueue(qu);//初始化队列  
  enQueue(qu,b);//根结点指针进入队列
  while(!QueueEmpty(qu)){//队不为空，则循环  
  deQueue(qu,p);//出队结点p
  printf("%c",p->data);//访问结点p
  if(p->lchild!=NULL)enQueue(qu,p->lchild);//有左孩子时将其进队
  if(p->rchild!=NULL)enQueue(qu,p->rchild);//有右孩子时将其进队
  }
}

二叉树的建立-遍历算法的应用

Status CreateBiTree(BiTree &T){
  scanf(&ch);
  if(ch=="#")T=NULL;
  else{
    if(!(T=(BiTNode*)malloc(sizeof(BiTNode))))exit(OVERFLOW);
    T->data=ch;//生成根结点  
    CreateBiTree(T->lchild);//构造左子树
    CreateBiTree(T->rchild);//构造右子树
  }
  return OK;
}

复制二叉树-遍历算法的应用

如果是空树，递归结束
否则，申请新结点空间，复制根结点
递归复制左子树
递归复制右子树

int Copy(BiTree T,BiTree &NewT){
  if(T==NULL){
    NewT=NULL;
    return 0;
  }
  else {
    NewT=new BiTNode;
    NewT->data=T->data;
    Copy(T->lChild,NewT->lchild);
    Copy(T->rChild,NewT->rchild);
  }
}

计算二叉树深度-遍历算法的应用

int Depth(BiTree T){
  if(T==NULL){
    return 0;
  }
  else {
    m=Depth(T->lChild);
    n=Depth(T->rChild);
    if(m>n)return(m+1);
    else return (n+1);
  }
}

计算二叉树节点总数-遍历算法的应用

int NodeCount(BiTree T){
  if(T==NULL){
    return 0;
  }
  else 
  return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
}

计算二叉树叶子节点总数-遍历算法的应用

int LeadCount(BiTree T){
  if(T==NULL){
    return 0;
  }
  if(T->lchild==NULL &&T->rchild==NULL)return 1;
  else 
  return LeafCount(T->lchild)+LeafCount(T->rchild);
}

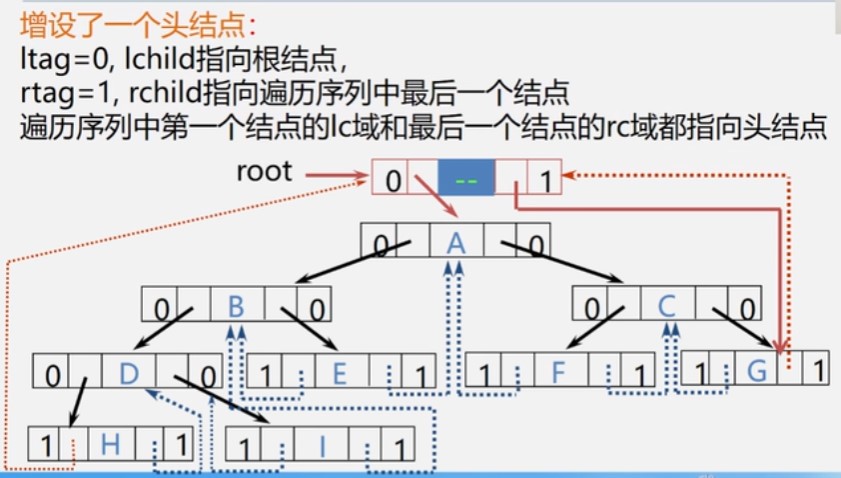
线索二叉树

当用二叉链表作为二叉树的存储结构时，可以很方便的找到某个结点的左右孩子；但一般情况下，无法直接找到该结点在某种遍历序列中的前驱和后继结点

解决方法：

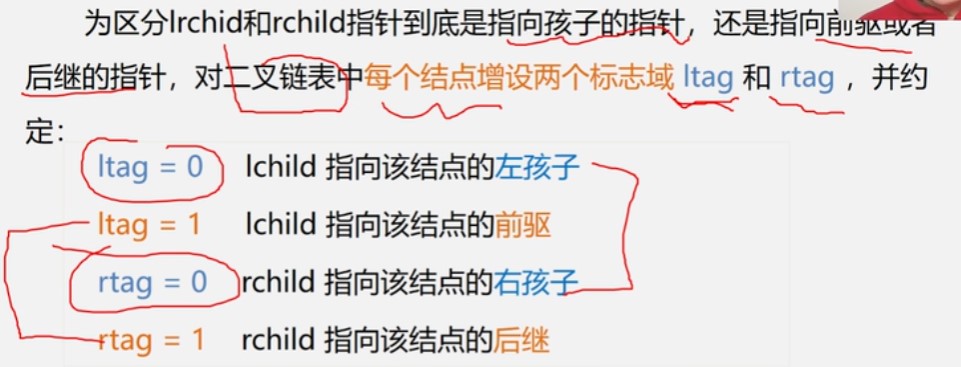
typedef struct BiThrNode{
  int data;
  int ltag,rtag;
  struct BiThrNode *lchild,rchild;
}BithrNode,*BiThrTree;

树和森林

森林：是m棵互不相交的树的集合
树和森林可以相互转化

树的存储结构

双亲表示法

实现：定义结构数组，存放树的结点，每个结点两个域：
1.数据域：存放结点本身信息
2.双亲域：指示本结点的双亲结点在数组中的位置

类型描述：

typedef struct PTNode{ 
  TElemType data;
  int parent;//双亲位置域
}PTNode;

树结构：

#define MAX_TREE_SIZE 100
typedef struct PTNode{ 
  PTNode nodes[MAX_TREE_SIZE];
  int r,n;//根结点的位置和结点个数
}PTree;

孩子链表

孩子结点结构：

typedef struct CTNode{ 
  int child;
  struct CTNode *next;
}*ChildPtr;

双亲结点结构：

typedef struct{ 
  TElemType data;
  ChildPtr firstchild;//孩子链表头指针
}CTBox;

树结构：

#define MAX_TREE_SIZE 100
typedef struct { 
  }CTBox nodes[MAX_TREE_SIZE];
  int r,n;//根结点的位置和结点个数
}CTree;

带双亲的孩子链表：两种模式的混合

孩子兄弟表示法