关系数据库
关系数据结构及形式化定义
单一的数据结构:关系
现实世界的实体以及实体间的各种联系均用关系来表示
逻辑结构:二维表
从用户角度,关系模型中数据的逻辑结构是一张二维表
建立在集合代数的基础上
域(Domain):一组具有相同数据类型的值的集合
- 整数
- 实数
- 介于某取值范围的整数
- 指定长度的字符串集合
- …
笛卡尔积(Cartesian Product):给定一组域$D_1,D_2,…D_n$,这些域中可以有相同的
$D_1,D_2,…D_n$的笛卡尔积为:
$D_1×D_2×..×D_n= ${$(d_1,d_2,…,d_n)|d_i\in D_i,i=1,2,…,n$}所有域的所有取值的一个组合
给定两个集合 $A$ 和 $B$,其笛卡尔积 $A \times B$ 定义为由所有有序对 $(a, b)$ 组成的集合,其中 $a \in A$,$b \in B$。也就是说,$A \times B$ 包含所有形如 $(a, b)$ 的有序对,其中 $a$ 是 $A$ 中的元素,$b$ 是 $B$ 中的元素。
例如,如果 $A = {1, 2}$,$B = {3, 4}$,则 $A \times B$ 包含以下有序对:$(1, 3)$,$(1, 4)$,$(2, 3)$ 和 $(2, 4)$。
不能重复
元组(Tuple):
笛卡尔积中每一个元素$(d_1,d_2,…,d_n)$叫作一个n元组(n-tuple)或简称元组(Tuple)
(张清玫,计算机专业,李勇)、(张清玫,计算机专业,刘晨)等都是元组
分量(Component):
笛卡尔积元素$(d_1,d_2,…,d_n)$中的每一个值$d_i$叫作一个分量
张清玫、计算机专业、李勇、刘晨等都是分量
基数(Cardinal number):
若$D_i(i=1,2,…,n)$为有限集,其基数为$m_i(i=1,2,…,n)$,则$D_1×D_2×..×D_n$的基数$M$为
$M=\prod_{i=1}^n{m_i} $
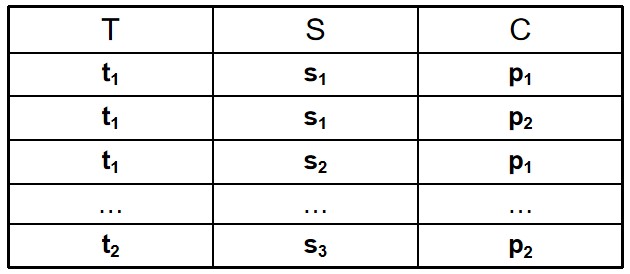
例:设
$D_1$为教师集合(T)= {t1,t2}
$D_2$为专业集合(S)= {s1,s2 ,s3}
$D_3$为研究生集合(P)= {p1,p2}
则$D_1×D_2×D_3$是个三元组集合,元组个数为$2\times3\times2$,是所有可能的(教师,专业,研究生)元组集合
关系(Relation):
$D_1,D_2,…,D_n$的笛卡尔积的某个子集才有实际含义,例如上面所示的笛卡尔积,只有取出有实际意义的元组来构造关系
关系
$D_1×D_2×..×D_n$的子集叫作在域$D_1,D_2,…,D_n$上的关系,表示为
$R(D1,D2,…,Dn)$
- $R$:关系名
- $n$:关系的目或度(Degree)
元组
关系中的每个元素是关系中的元组,通常用t表示
单元关系与二元关系
当n=1时,称该关系为单元关系(Unary relation)或一元关系
当n=2时,称该关系为二元关系(Binary relation)
关系的表示
关系也是一个二维表,表的每行对应一个元组,表的每列对应一个域

属性
关系中不同列可以对应相同的域
为了加以区分,必须对每列起一个名字,称为属性(Attribute)
n目关系必有n个属性
码
候选码(Candidate key)
若关系中的某一属性组的值能唯一地标识一个元组,则称该属性组为候选码
简单的情况:候选码只包含一个属性
全码(All-key)
最极端的情况:关系模式的所有属性组是这个关系模式的候选码,称为全码(All-key)
主码
若一个关系有多个候选码,则选定其中一个为主码(Primary key)
主属性
候选码的诸属性称为主属性(Prime attribute)不包含在任何侯选码中的属性称为非主属性( Non-Prime attribute)或非码属性(Non-key attribute)
例:哪些属性是候选码、主码、主/非主属性?(假设学生没有重名)
学生(**学号,姓名**,性别,班号)
选课(**学号,课程号**,成绩)
三类关系
基本关系(基本表或基表)
实际存在的表,是实际存储数据的逻辑表示
查询表
查询结果对应的表
视图表
由基本表或其他视图表导出的表,是虚表,不对应实际存储的数据
基本关系的性质
基本关系的性质
- 列是同质的(Homogeneous)
- 不同的列可出自同一个域,用属性名区分
- 列的顺序无所谓,列的次序可以任意交换
- 任意两个元组的候选码不能相同
- 行的顺序无所谓,行的次序可以任意交换
- 分量必须取原子值
关系模式:
是型,是对关系的静态、稳定描述,包括:
- 元组集合的结构
- 元组语义以及完整性约束条件
- 属性间的数据依赖关系集合
关系模式可以形式化地表示为:$R(U,D,DOM,F)$
- $R$ 关系名
- $U$ 组成该关系的属性名集合
- $D $ 属性组$U$中属性所来自的域
- $DOM$ 属性向域的映象集合
- $F$ 属性间的数据依赖关系集合
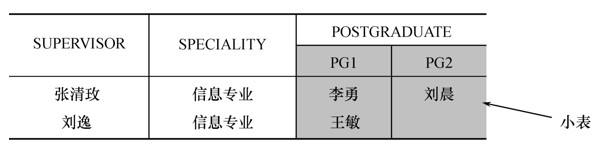
例:
导师和研究生出自同一个域——人,取不同的属性名,并在模式中定义属性向域的映象:
DOM(SUPERVISOR)= PERSON,DOM(POSTGRADUATE)= PERSON
关系模式通常可以简记为 : $R (U) $ 或 $ R (A_1,A_2,…,A_n)$
- $R$: 关系名
- $A_1,A_2,…,A_n $ : 属性名
注:
域名及属性向域的映象常常直接说明为属性的类型、长度
例如:学生(学号,姓名,性别,班号)
关系数据库的型与值
关系数据库的型:关系数据库模式,对关系数据库的描述,包括
- 若干域的定义
- 在这些域上定义的若干关系模式
关系数据库的值: 关系模式在某一时刻对应的关系的集合,简称为关系数据库
例如选课数据库的模式:
学生(学号,姓名,性别,班号)
选课(学号,课程号,成绩)
课程(课程号,课程名,学分)
关系操作
- 基本关系操作
- 常用的关系操作
- 查询:选择、投影、连接、除、并、交、差
- 数据更新:插入、删除、修改
- 查询的表达能力是其中最主要的部分
- 选择、投影、并、差、笛卡尔基是5种基本操作
- 关系操作的特点
- 集合操作方式:操作的对象和结果都是集合,一次一集合的方式
- 高度非过程化:只要指出“做什么”,不需要描述“怎么做”
- 常用的关系操作
- 关系数据库语言的分类
- 关系代数语言
- 用对关系的运算来表达查询要求
- 代表:ISBL
- 关系演算语言:用谓词来表达查询要求
- 域关系演算语言
- 谓词变元的基本对象是域变量
- 代表:QBE
- 元组关系演算语言
- 谓词变元的基本对象是元组变量
- 代表:APLHA, QUEL
- 域关系演算语言
- 关系代数和关系演算是相互等价的
- 具有关系代数和关系演算双重特点的语言
- 代表:SQL(Structured Query Language)
- 关系代数语言
关系代数
概述
什么是关系代数?
- 关系数据库的一种抽象的查询语言,用对关系的运算来表达查询。
- 关系代数
- 运算对象:关系
- 运算符:关系运算符
- 代数的要素:运算对象、运算符。
- 运算符连接运算对象和/或表达式形成表达式
为什么要学关系代数?
- 已不用作商用RDBMS的查询语言,但SQL语言以关系代数作为核心
- RDBMS处理查询时,首先将SQL查询翻译成关系代数或相似的内部表示
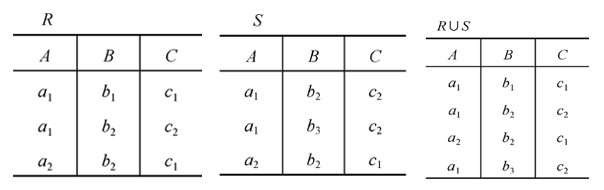
传统的集合运算
并
R和S
- 具有相同的目n(即两个关系都有n个属性)
- 相应的属性取自同一个域
R∪S
仍为n目关系,由属于R或属于S的元组组成
$R∪S =$ { $t|t \in R ∨ t \in S $}
交
R和S
- 具有相同的目n
- 相应的属性取自同一个域
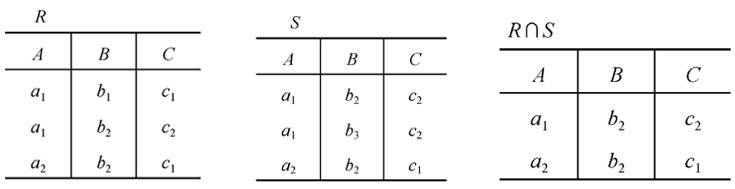
R∩S
仍为n目关系,由既属于R又属于S的元组组成
$R∩S =$ { $t|t \in R ∧ t \in S $}
差
R和S
- 具有相同的目n
- 相应的属性取自同一个域
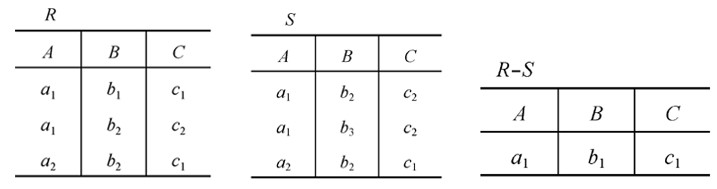
R - S
仍为n目关系,由属于R而不属于S的所有元组组成
$R-S =$ { $t|t \in R ∧ t \notin S $}
笛卡尔积
严格地讲应该是广义的笛卡尔积
R: n目关系,k1个元组
S: m目关系,k2个元组
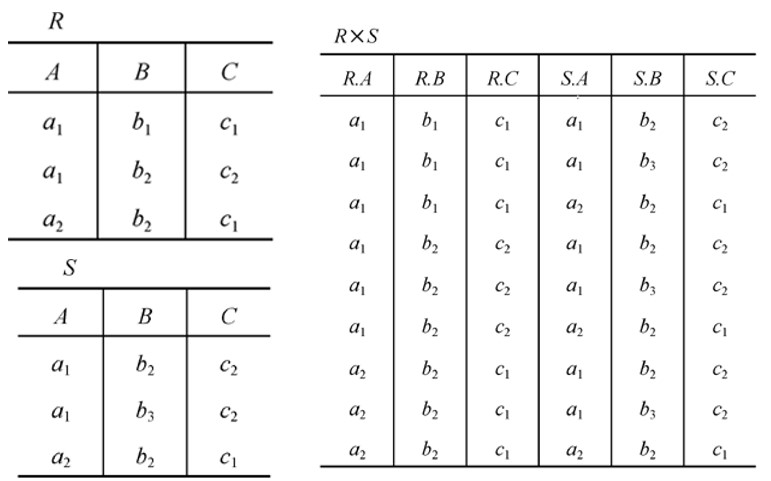
R×S
- 列:(n+m)列元组的集合
- 元组的前n列是关系R的一个元组
- 后m列是关系S的一个元组
- 行:k1×k2个元组
- $R\times S =$ { $t_rt_s|t_r \in R ∧ t_s \in S $}
- 列:(n+m)列元组的集合
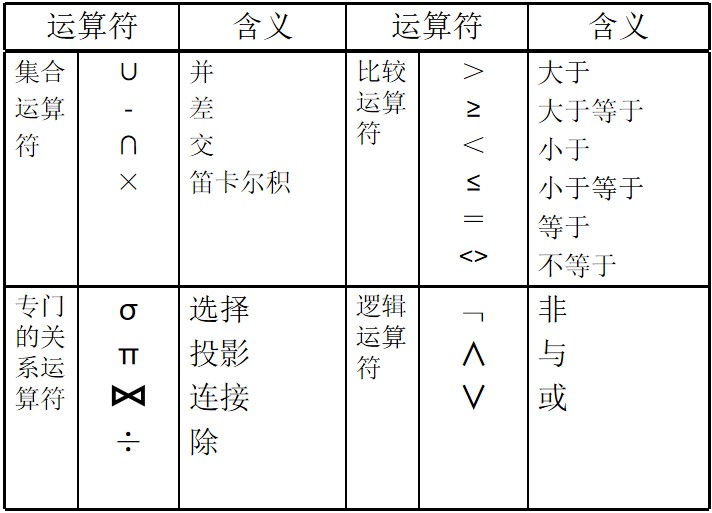
专门的关系运算
选择运算
在关系R中选择满足给定条件的元组
$\sigma_{F(R)}$$=${$t | t \in R ^{F(t)} = 真$}
F是选择的条件,$\forall t\in R$,F(t)要么为真,要么为假
- F的形式:由逻辑运算符$( \vee,\wedge,\neg)$连接关系表达式而成
关系表达式:$X \theta Y$
X,Y是属性名、常量、或简单函数
$\theta$是比较算符,$\theta \in${$\leq,\geq,\neq,=,>,< $}
例如:
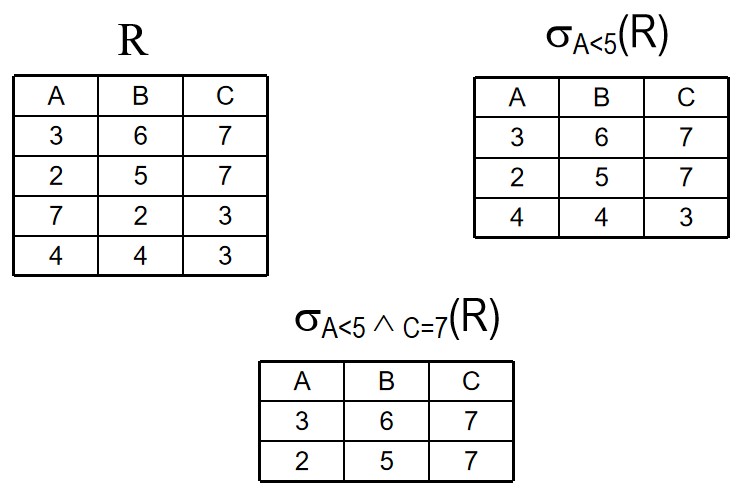
再如:
找年龄不小于20的男学生
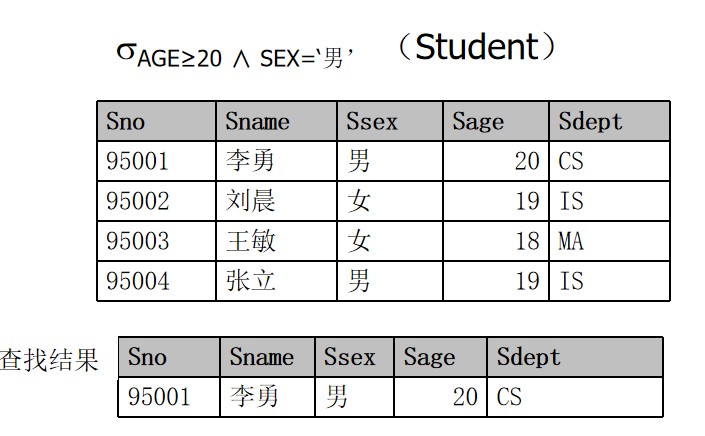
又如:
查找信息系(IS系)的全体学生
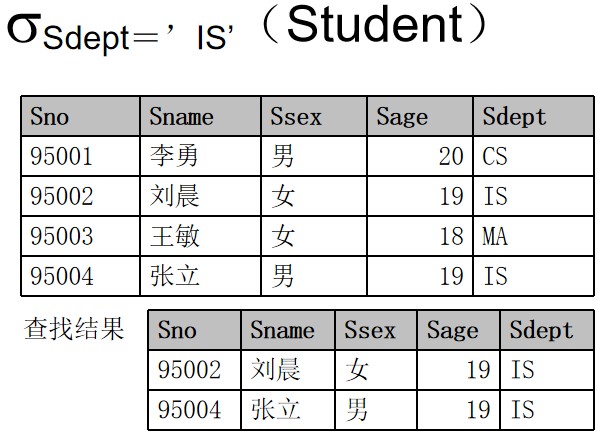
投影
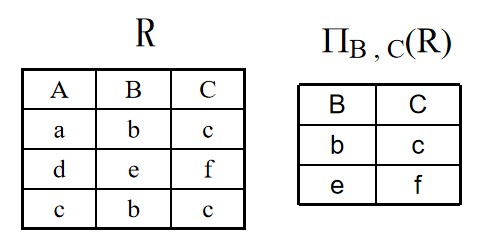
从关系R中取若干列组成新的关系(从列的角度)
$\Pi^{A(R)} = ${ $t[A] | t\in R $} $, A\subseteq R$
其中A为R的属性列
投影的结果中要去掉相同的行
例如:
选择与投影的对比
选择运算是从关系R中选取使逻辑表达式F为真的元组,是从行的角度进行的运算
投影操作主要是从列的角度进行运算
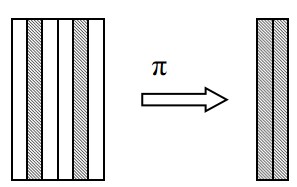
例如:找95001号学生所选修的课程号$\Pi_{Cno}(\sigma_{Sno=95001}(SC))$
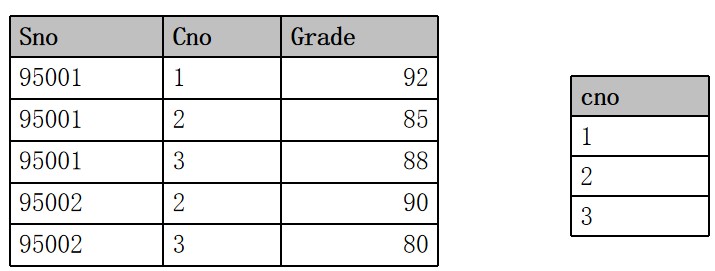
连接
连接操作是从两个关系的广义笛卡尔积中选择属性间满足一定条件的元组。通常写为:
$R \Join S {A\theta B}= \sigma{R.A\theta S.B}(R\times S)$
A,B为R和S上度数相等且可比的属性列,$\theta$为比较运算符
例如:
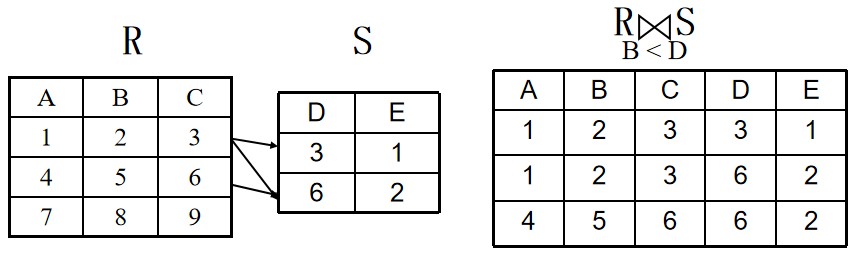
θ为“=”的连接运算称为等值连接 :
等值连接的含义:从关系R与S的广义笛卡尔积中选取A、B属性值相等的那些元组,即等值连接为:
$R \Join S _{A= B}=${ $ t_rt_s | t_r \in R ∧ t_s \in S ∧ t_r[A] = t_s[B] $}
若R和S具有相同的属性组(来自相同的域,表示相同的含义),且连接的运算符θ为“=”,并且在连接的结果中去掉重复的属性组,这种连接称为自然连接:
记为:
$R \Join S$ (当R与S无相同属性时,$R \Join S$ =$ R×S$)
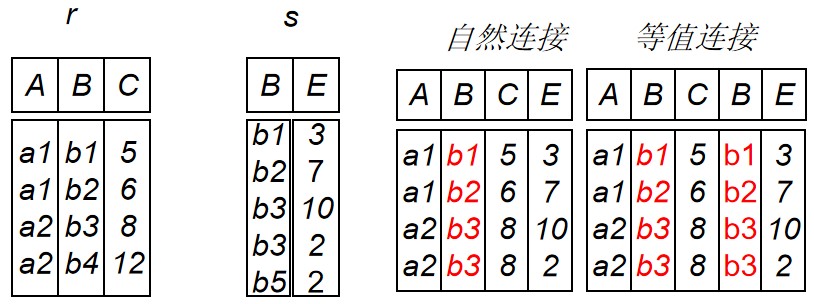
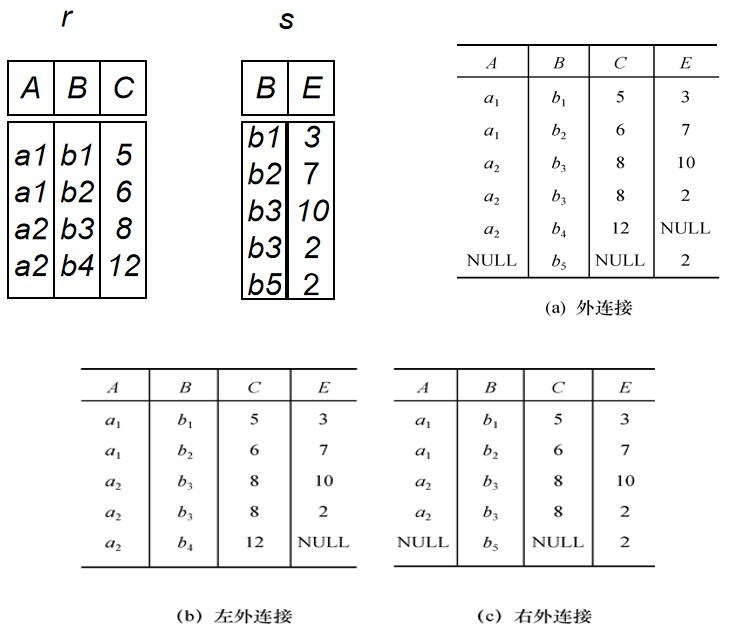
外连接
如果把舍弃的元组也保存在结果关系中,而在其他属性上填空值(Null),这种连接就叫做外连接(OUTER JOIN)。
左外连接
如果只把左边关系R中要舍弃的元组保留就叫做左外连接(LEFT OUTER JOIN或LEFT JOIN)
右外连接
如果只把右边关系S中要舍弃的元组保留就叫做右外连接(RIGHT OUTER JOIN或RIGHT JOIN)
一般的连接操作是从行的角度进行运算。
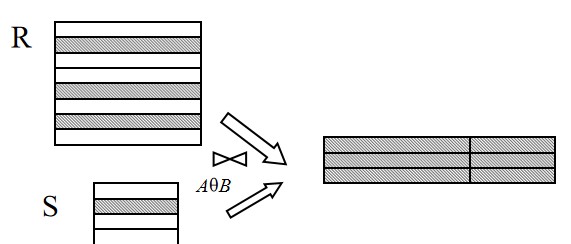
自然连接还需要取消重复列,所以是同时从行和列的角度进行运算。
同样是对两个关系进行合并操作,连接运算和集合交/并运算有何区别?
连接运算是基于两个关系之间的共同属性进行操作的。连接运算将两个关系中满足某种条件的元组组合起来形成一个新的关系。连接运算常用的有内连接、外连接、自然连接等。连接运算的结果是两个关系的交集,但是只包含那些满足连接条件的元组。连接运算的目的是为了寻找关系之间的联系,以便进行数据的查询和分析。
集合交/并运算是将两个关系中的元组进行组合,形成一个新的关系。集合交/并运算的结果是两个关系的交集或并集。集合运算中的交集操作得到的结果是两个关系中共同元素的集合,而并集操作得到的结果是两个关系中所有元素的集合。集合运算的目的是为了去除重复元素或者将多个数据源合并成一个数据源,以便进行数据分析或处理。
一些方法:
==单表第一步先选择,第二步再投影==
==多表先选再连后投影==
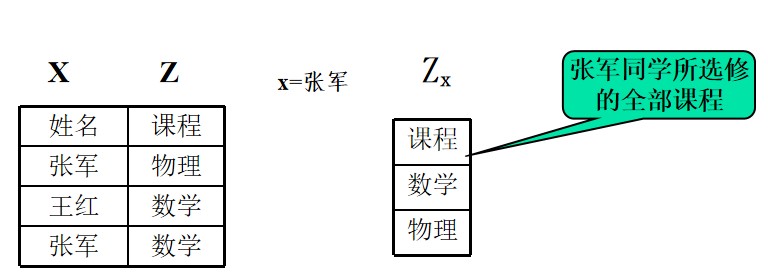
象集
关系R(X , Z), X, Z是属性组,x是X上的取值,定义x在R中的象集为
$Z_X${ $ t_{[Z] } | t \in R ∧ t_{[X]} =X $}
从R中选出在X上取值为x的元组,去掉X上的分量,只留Z上的分量
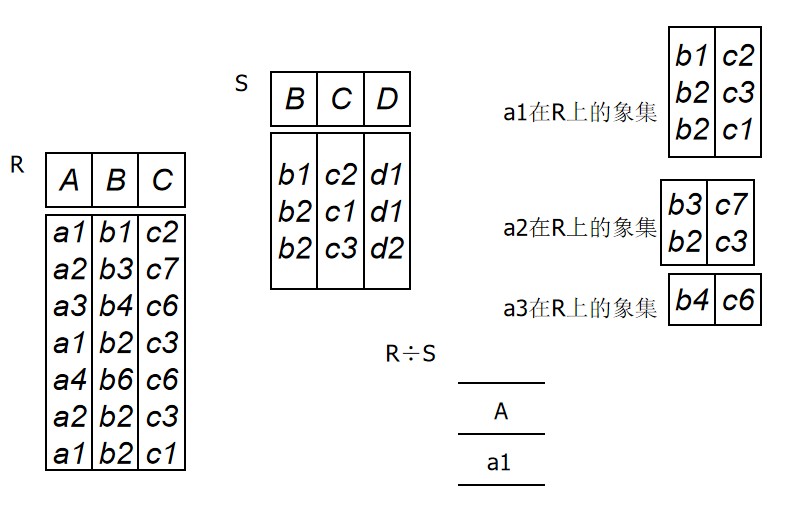
除运算
给定关系R(X,Y)和S(Y,Z),其中X,Y,Z为属性组。R中的Y与S中的Y可以有不同的属性名,但必须出自相同的值域。
R与S的除运算得到一个新的关系P(X),P是R中满足下列条件的元组在X属性列上的投影:元组在X上分量值x的象集Yx包含S在Y上投影的集合。记做:
$R \div S =${ $ t_r[X] | t_r \in R ∧ \Pi_Y(S)\subseteq Y_X $}
例:
例: 查询选修了全部课程的学生号码和姓名
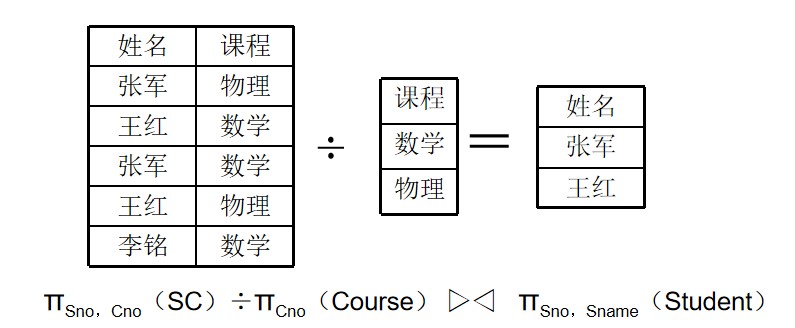
例:查询至少选修1号课程和3号课程的学生号码

重命名运算
关系代数运算的结果没有可供引用的名字,使得复杂的查询显得非常冗长
用小写希腊字母$\rho$表示的命名运算可对关系更名,或赋予关系代数运算结果一个名字:
对给定的关系代数表达式E,表达式$\rho_ x(E)$返回表达式E的结果,并把名字x赋给了它。
假设关系代数表达式E是n元的,则表达式:$\rho_ {x(A_1,A_2,…,A_n)}(E)$
返回表达式E的结果,并赋给它名字x,同时将E的各属性更名为$A_1,A_2,…,A_n$
例:
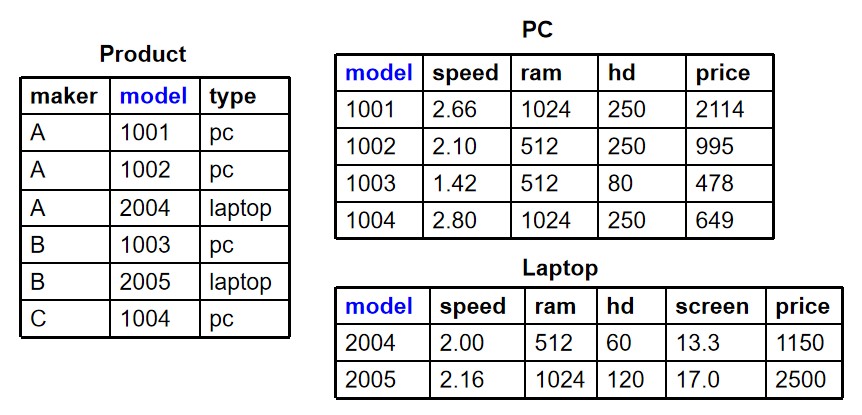
1.查询至少出现在两款PC中的硬盘容量
$\Pi_{PC1.hd}(\rho_{PC1}(PC) \Join {PC1.hd=PC2.hd\wedge PC1.model\neq PC2.model }\rho{PC2}(PC) )$
注释:
- $\rho_{PC1}(PC)$: 对关系PC 进行重命名操作,将其重命名为PC1
- $\rho_{PC2}(PC)$: 对关系PC 进行重命名操作,将其重命名为PC2
- $PC1 \Join_{PC1.hd=PC2.hd\wedge PC1.model\neq PC2.model} PC2$: 对重命名后的PC1和PC2进行自然连接操作,连接条件为PC1.hd等于PC2.hd并且PC1.model不等于PC2.model
- $\Pi_{PC1.hd}(\cdot)$:对连接结果进行投影操作,只保留PC1.hd属性
因此,最终的关系代数表达式表示的是:从关系PC中选择两个不同型号但硬盘容量相同的计算机,仅保留它们的硬盘容量属性,并且重命名为PC1.hd
2.查询至少生产两款不同速度PC的制造商
$\Pi_{R1.maker}(\rho_{R1}(Product \Join PC) \Join {R1.speed\neq R2.speed\wedge R1.maker= R2.maker }\rho{R2}(Product \Join PC) )$
注释:
- $\rho_{R1}(Product \Join PC)$: 将关系Product和PC进行自然连接操作,并将结果重命名为R1。
- $\rho_{R2}(Product \Join PC)$: 将关系Product和PC进行自然连接操作,并将结果重命名为R2。
- $R1 \Join_{R1.speed\neq R2.speed\wedge R1.maker= R2.maker} R2$: 对重命名后的R1和R2进行自然连接操作,连接条件为R1.speed不等于R2.speed并且R1.maker等于R2.maker。
- $\Pi_{R1.maker}(\cdot)$: 对连接结果进行投影操作,只保留R1.maker属性。
因此,最终的关系代数表达式表示的是:从关系Product和PC中选择制造商相同,但是速度不同的产品,仅保留它们的制造商属性,并将结果重命名为R1.maker。
关系的完整性
关系的三类完整性约束
实体完整性和参照完整性:
关系模型必须满足的完整性约束条件
称为关系的两个不变性,应该由关系系统自动支持
用户定义的完整性:
应用领域需要遵循的约束条件,体现了具体领域中的语义约束
实体完整性
若属性A是基本关系R的主属性,则属性A不能取空值
例如:
SAP(SUPERVISOR,SPECIALITY,POSTGRADUATE)
POSTGRADUATE:
主码(假设研究生不会重名)
不能取空值
实体完整性规则是针对基本关系而言的
- 一个基本表通常对应现实世界的一个实体集。
- 现实世界中的实体是可区分的,即它们具有某种唯一性标识。
- 关系模型中以主码作为唯一性标识。
- 主码中的属性即主属性不能取空值。主属性取空值,就说明存在某个不可标识的实体,即存在不可区分的实体,这与第2点相矛盾,因此这个规则称为实体完整性
参照完整性
关系间的引用
在关系模型中实体及实体间的联系都是用关系来描述的,因此可能存在着关系与关系间的引用
例1:
学生实体、专业实体
学生(学号,姓名,性别,专业号,年龄) 专业(专业号,专业名)
注:主码
学生关系引用了专业关系的主码“专业号”。
学生关系中的“专业号”值必须是确实存在的专业的专业号 ,即专业关系中有该专业的记录。
例2:
学生、课程、学生与课程之间的多对多联系
学生(学号,姓名,性别,专业号,年龄)
课程(课程号,课程名,学分)
选修(学号,课程号,成绩)
例3:
学生实体及其内部的一对多联系
学生(学号,姓名,性别,专业号,年龄,班长)
“学号”是主码,“班长”是外码,它引用了本关系的“学号”
“班长” 必须是确实存在的学生的学号
外码
设F是基本关系R的一个或一组属性,但不是关系R的码。
如果F与基本关系S的主码$K_s$相对应,则称F是基本关系R的外码
基本关系R称为参照关系(Referencing Relation)
基本关系S称为被参照关系(Referenced Relation)或目标关系(Target Relation)
例1:学生关系的“专业号”与专业关系的主码“专业号”相对应
“专业号”属性是学生关系的外码
专业关系是被参照关系,学生关系为参照关系
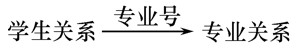
例2:选修关系的“学号” 与学生关系的主码“学号”相对应
选修关系的“课程号”与课程关系的主码“课程号”相对应
“学号”和“课程号”是选修关系的外码
学生关系和课程关系均为被参照关系选
修关系为参照关系

例3:“班长”与本身的主码“学号”相对应
“班长”是外码
学生关系既是参照关系也是被参照关系
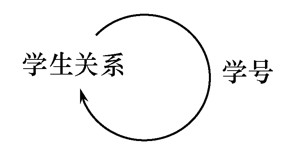
关系R和S不一定是不同的关系
目标关系S的主码Ks 和参照关系的外码F必须定义在同一个(或一组)域上
外码并不一定要与相应的主码同名
当外码与相应的主码属于不同关系时,往往取相同的名字,以便于识别
参照完整性规则
若属性(或属性组)F是基本关系R的外码,它与基本关系S的主码Ks相对应(基本关系R和S不一定是不同的关系),则对于R中每个元组在F上的值必须为:
- 或者取空值(F的每个属性值均为空值)
- 或者等于S中某个元组的主码值
例1:学生关系中每个元组的“专业号”属性只取两类值:
空值,表示尚未给该学生分配专业
非空值,这时该值必须是专业关系中某个元组的“专业号”值,表示该学生不可能分配一个不存在的专业
例2:选修(学号,课程号,成绩)
“学号”和“课程号”可能的取值 :
选修关系中的主属性,不能取空值
只能取相应被参照关系中已经存在的主码值
例3:学生(学号,姓名,性别,专业号,年龄,班长)
“班长”属性值可以取两类值:
(1)空值,表示该学生所在班级尚未选出班长
(2)非空值,该值必须是本关系中某个元组的学号值
用户定义的完整性
针对某一具体关系数据库的约束条件,反映某一具体应用所涉及的数据必须满足的语义要求
关系模型应提供定义和检验这类完整性的机制,以便用统一的系统的方法处理它们,而不要由应用程序承担这一功能
例子:
课程(课程号,课程名,学分)
“课程号”属性必须取唯一值
非主属性“课程名”也不能取空值
“学分”属性只能取值{1,2,3,4,5}



