线性规划模型
题目要求:
某工厂需要利用三种原材料(分别记为1、2、3)混合调配出三种不同的产品(甲、乙、丙)。具体材料要求及产品利润如下表所示。请建立数学模型,为该厂安排生产规划,使其利润最大。
产品名称 规格要求 单价 甲 原材料1不少于50%,原材料2不超过25% 50 乙 原材料1不少于25%,原材料2不超过50% 35 丙 不限 25
原材料名称 每天最多供应量 单价 1 100 65 2 100 25 3 60 35
变量说明
设变量$x_{ij}$:产品$i$中的原材料$j$的含量,其中$i$为产品名称(1对应甲,以此类推),$j$为原材料名称
模型建立
该问题要求求解利润最大时的生产规划安排,其中利润=收入-成本,我们利用线性规划模型进行求解:
目标函数:
$max_z=50(x_{11}+x_{12}+x_{13})+35(x_{21}+x_{22}+x_{23})+25(x_{31}+x_{32}+x_{33})-65(x_{11}+x_{21}+x_{31})-25(x_{12}+x_{22}+x_{32})-35(x_{13}+x_{23}+x_{33})$
其中:
$50(x_{11}+x_{12}+x_{13})+35(x_{21}+x_{22}+x_{23})+20(x_{31}+x_{32}+x_{33})$ 为总收入
$65(x_{11}+x_{21}+x_{31})+25(x_{12}+x_{22}+x_{32})+35(x_{13}+x_{23}+x_{33})$为总成本
约束条件:
$ x_{11}≥0.5(x_{11}+x_{12}+x_{13})$
对于产品甲,原材料1不少于50%
$ x_{12}+x_{13}-x_{11}≤0$
$ x_{12}≤0.25(x_{11}+x_{12}+x_{13})$
对于产品甲,原材料2不超过25%
$3x_{12}-x_{11}-x_{13}≤0$
$x_{21}≥0.25(x_{21}+x_{22}+x_{23})$
对于产品乙,原材料1不少于25%
$x_{22}+x_{23}-3x_{21}≤0$
$ x_{22}≤0.5(x_{21}+x_{22}+x_{23})$
对于产品乙,原材料2不超过50%
$x_{22}-x_{21}-x_{23}≤0$
$x_{11}+x_{21}+x_{31}≤100$
对于原料1,每天最多供应量为100
$x_{12}+x_{22}+x_{32}≤100$
对于原料2,每天最多供应量为100
$x_{13}+x_{23}+x_{33}≤60$
对于原料3,每天最多供应量为60
$x_{ij}≥0,(i,j=1,2,3)$
模型求解
我们将公式简化成Matlab代码
C=[15 -25 -15 30 -10 0 40 0 10]; A=[-1 1 1 0 0 0 0 0 0;-1 3 -1 0 0 0 0 0 0;0 0 0 -3 1 1 0 0 0;0 0 0 -1 1 -1 0 0 0;1 0 0 1 0 0 1 0 0;0 1 0 0 1 0 0 1 0;0 0 1 0 0 1 0 0 1]; b=[0 0 0 0 100 100 60]; Aeq= []; beq= []; LB= zeros(9,1); UB= []; [x,fval]= linprog(C,A,b,Aeq,beq,LB,UB);
模型结果
运行后结果如下:
其中x输出值: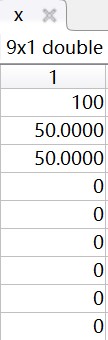 fval输出值为:
fval输出值为: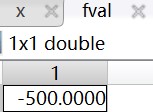
因此可得出结果:当生产安排为只生产甲产品且按照原材料1量100、原材料2量50、原材料3量50的规格进行制作时总利润最大,此时总利润为500



